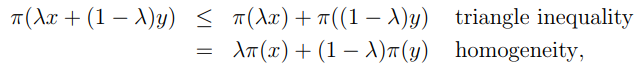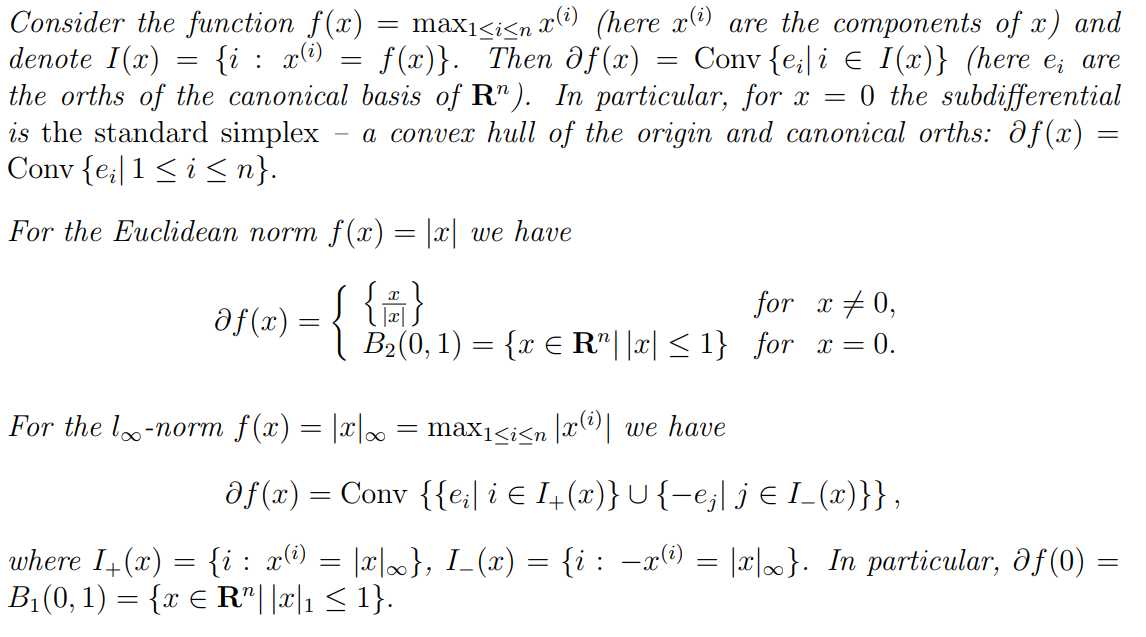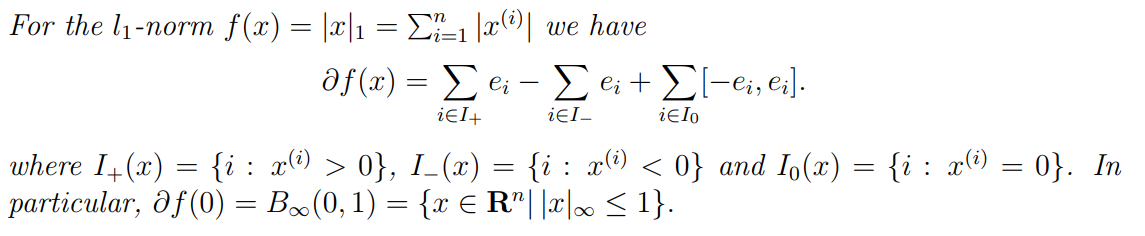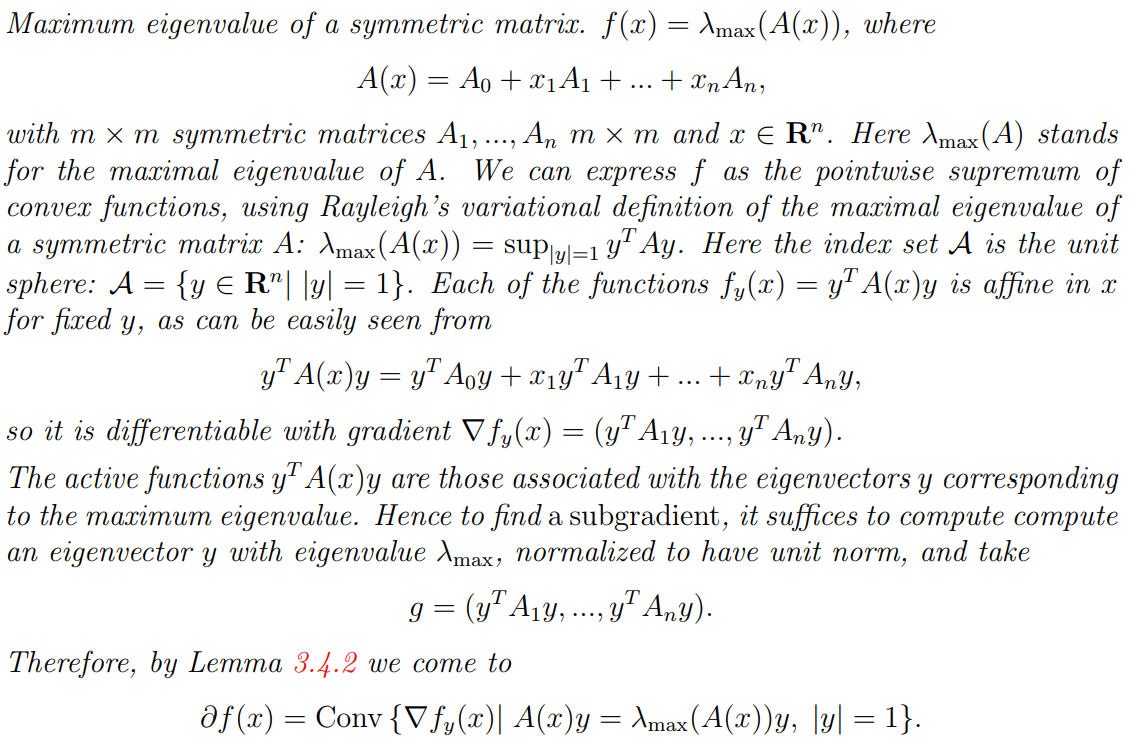CVX notes

Preliminaries

1. PSD

M is positive semidefinite matrix $⟺$ all principal submatrices $P$ of $M$ are PSD

Note: This follows by considering the quadratic form $x^{T}Mx$ and looking at the components of $x$ corresponding to the defining subset of principal submatrix. The converse is trivially true.

M is PSD $⟺$ all principal minors are non-negative (所有主子式非负)

将M写成二次型：

$$x^{T}Mx=\sum _{i,j}{M}_{ij}{x}_i{x}_j$$

于是取 $x$ 为标准基 $e_i⟹M_{ii}\ge 0⟹\mathbf{tr}(M)\ge 0$ , 再取$x$为零向量只有 i，j两个位置为 1，则

$$\begin{array}{c}{x}^{T}Mx=M_{ii}{M}_{jj}-M_{ij}^2\ge 0(PSD)\\ ⟹M_{ij}\le \sqrt{M_{ii}{M}_{jj}}\le \frac{M_{ii}+M_{jj}}{2}\end{array}$$

---

2. Matrix norm

General definition of a norm: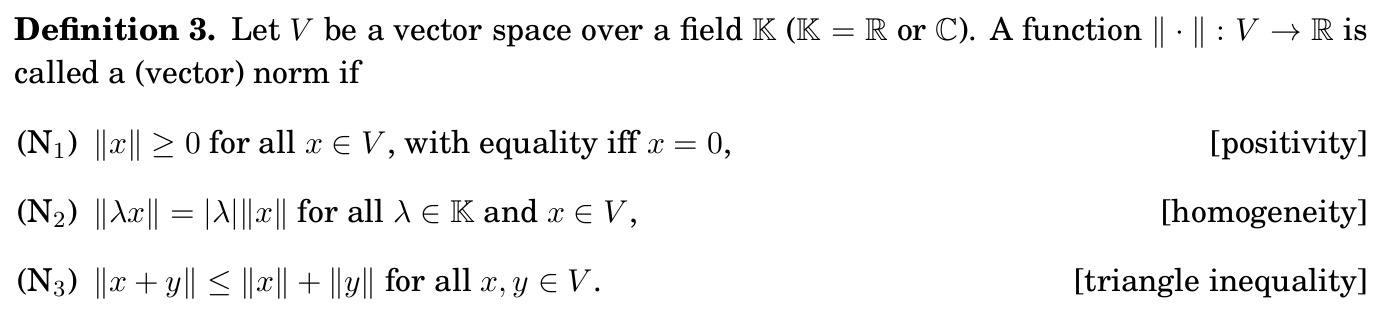

Matrix norm:

• Frobenius norm: $\Vert A{\Vert }_F:=\sqrt{⟨A,A{⟩}_F}=\sqrt{\mathbf{tr}(A^{\ast }A)}$
• Induced norm: \|A\|_p := \sup_\limits{\|x\|_p = 1} \|Ax\|_p
• Nuclear norm: $\Vert A{\Vert }_{nuclear}:=\sum {\sigma }_i(A)$ (奇异值之和)
• Spectral norm: $\Vert A{\Vert }_{spectral}:={\lambda }_1$ (最大特征值)

Spectrial radius

---

3. Duality

Two equivalent ways to represent a convex set:

• standard representation: The family of points in the set
• dual representation: The set of halfspaces containing the set (半平面的交集)

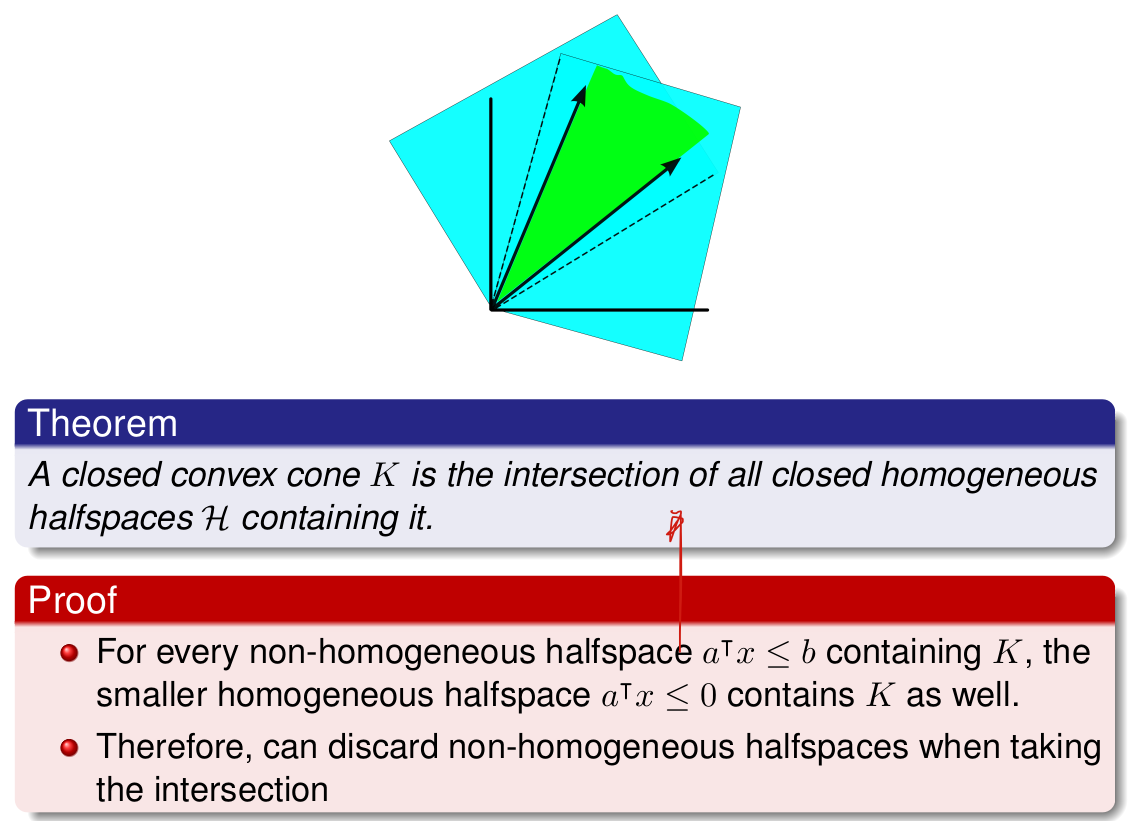
A closed convex set $S$ is the intersection of all closed halfspaces $H$ containing it.

Polar Let $S\subseteq {\mathbb{R}}^n$ be a convex set containing the origin. The polar of $S$ is defined as follows

$$S^{\circ }:=\{y|y^{T}x\le 1,\forall x\in S\}$$

Note

• polar is one way of representing the all halfspaces containing a convex set
• every halfspace $a^{T}x\le b$ with $b\ne 0$ can be written as a “normalized” inequality $y^{T}x\le 1$, by dividing by $b$
• $S^{\circ }$ can be thought of as the normalized representations of halfspaces containing $S$

Properties of the polar:

1. $S^{\circ \circ }=S$
2. $S^{\circ }$ is a closed convex set containing the origin
3. When 0 is in the interior of $S$, then $S^{\circ }$ is bounded
4. When $S$ is non-convex, $S^{\circ }=(\mathbf{conv}(S){)}^{\circ }$, and $S^{\circ \circ }=\mathbf{conv}(S)$

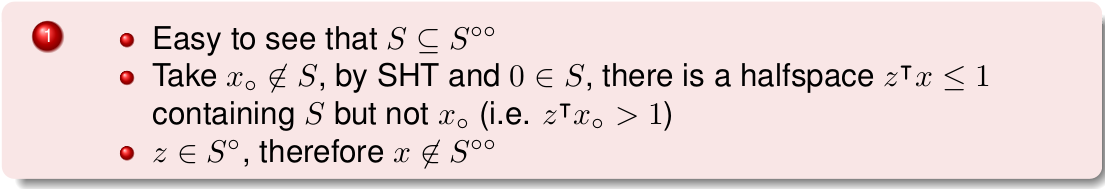
Polar duality of convex cones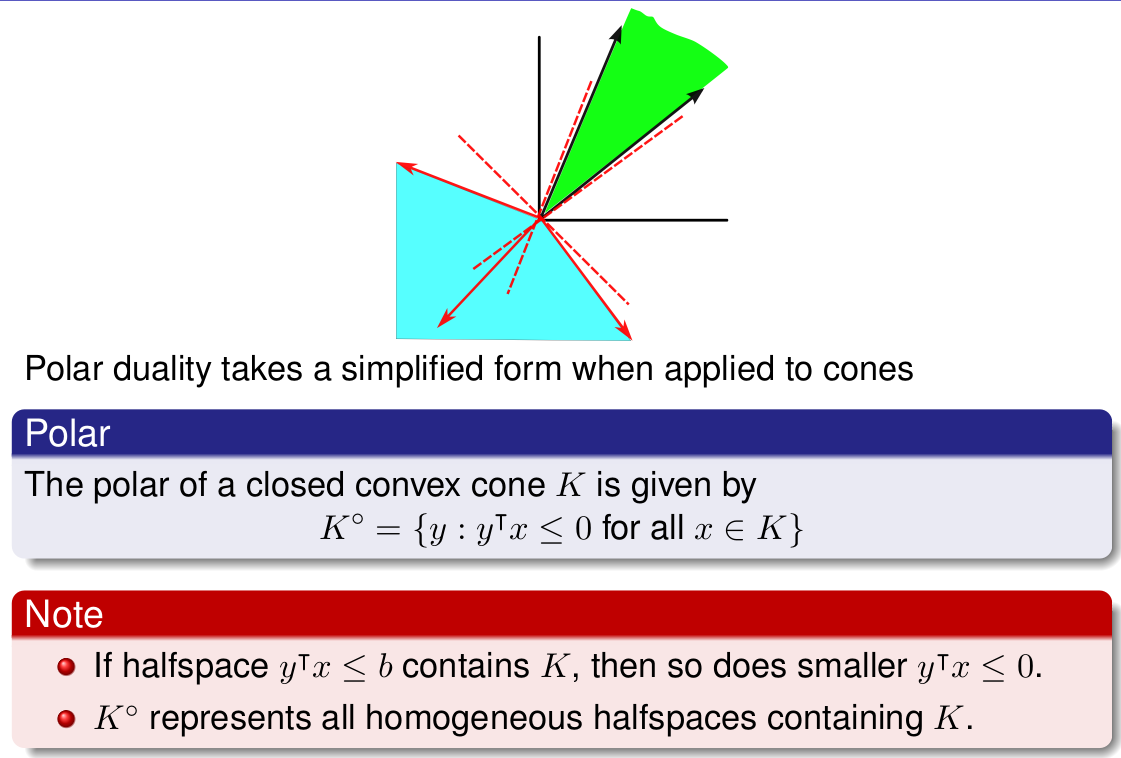

Notes

1. $K^{\circ \circ }=K$
2. $K^{\circ }$ is closed and convex

Conjugation of convex functions Let $f:{\mathbb{R}}^n\mapsto \mathbb{R}\cup \{\infty \}$ be a convex function. The conjugation of $f$ is

f^*(y) := \sup_\limits{x}(y^Tx - f(x))

Properties of the conjugate

1. $f^{\ast \ast }=f$
2. $f^{\ast }$ is convex (supremum of affine functions of $y$)

---

---

Convex sets

---

---

Convex functions

1. affine is convex: $f(x)=a^{T}x+b$

affine 既凸也凹

1. 任何范数是凸的

Proof: let $\pi (x)$ be a norm of $x$, then

2. $f$ is convex $⟺$ epi($f$) is convex

---

---

1. Closed convex

A convex function $f$ is called closed if its epigraph is a closed set.

1. $f$ which is convex and continuous on a closed domain is a closed function. (norms)

2. all differentiable convex functions are closed with dom$f={\mathbb{R}}^n$.

3. 当考虑一个凸函数时，通常认为在dom$f$外取值为$\infty$

4. Jensen’s inequality:

5. Corollary:

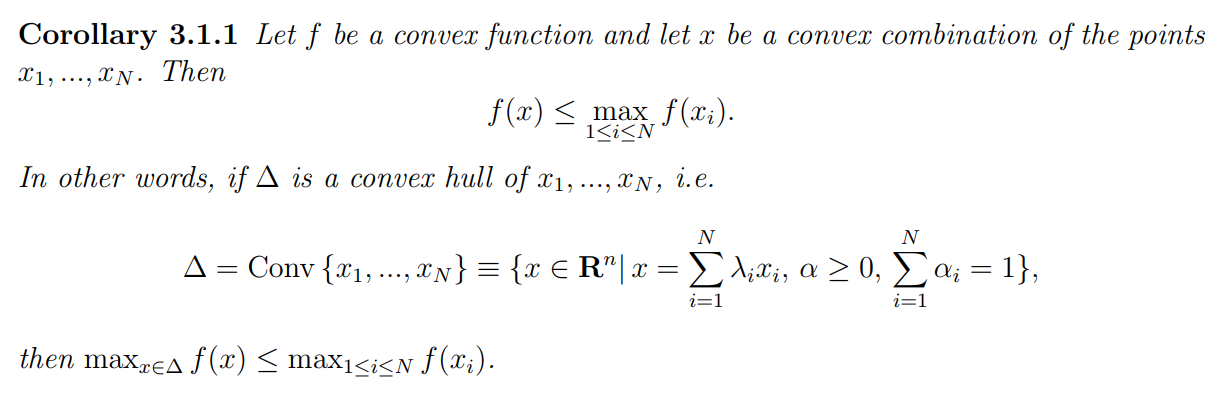
   pf: f(x) = f(\sum\alpha_i x_i) \le \sum \alpha_i f(x_i) \le \max_\limits{i} f(x_i)

---

2. Level sets

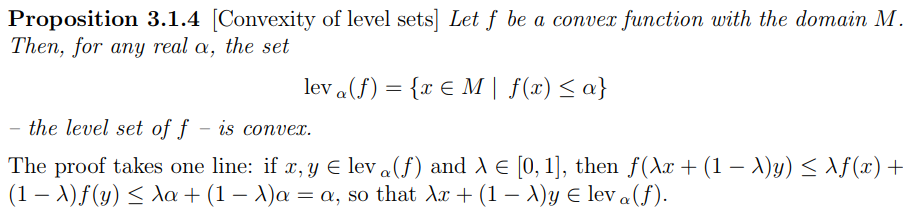
Note: the convexity of level sets does not characterize convex functions, but quasiconvex functions.

1. convex $f$ is closed $⟹$ all its level sets are closed

Some convex sets

1. norm ball ($\{x\in {\mathbb{R}}^n|\Vert x\Vert \le 1\}$) is convex and closed
2. 椭球($\{x|(x-a{)}^{T}Q(x-a)\le r^2\}$) is convex and closed

   pf: $x^{T}Qy:=⟨x,y⟩$ 满足内积的三条性质

   • bilinearity
   • symmetry
   • positivity 上述三条性质 $⟺$ Q is PSD

3. $ϵ$-neighborhood:

---

---

3. Operations perserving convexity of functions

1. stability under taking weighted sums: $f,g\mapsto \lambda f+\mu g,\lambda ,\mu \ge 0$
2. stability under affine substitutions of the argument: $x\mapsto Ax+b$ or $f(x)\mapsto \varphi (x)=f(Ax+b)$
3. stability under taking pointwise sup: \{f_i\}_{i \in \mathcal{I}} \mapsto g(x) := \sup_\limits{i \in \mathcal{I}}f_i(x), 凸函数族 $\{f_i{\}}_{i\in \mathcal{I}}$ 逐点取上确界而成的函数也是凸的
4. stability under partial minimization: $f(x,y)$ jointly convex in $(x,y)$, then g(x) = \inf_\limits{y} f(x,y) is convex (suppose g is proper, i.e., > -$\infty$ everywhere and is finite at least at one point)
5. stability under perspective: $f(x)\mapsto g(x,t)=tf(x/t),\mathbf{dom}g=\{(x,t)|x/t\in \mathbf{dom}f,t>0\}$

---

4. Detect convexity

Necessary and Sufficient Convexity Condition for smooth function:

• 一阶可微的光滑函数 $f$ 是凸的 $⟺$ $f^{\prime }(x)$ 单调非减
• 二阶可微的光滑函数 $f$ 是凸的 $⟺$ $f^{\prime \prime }(x)\ge 0$

subgradient property is characteristic of convex functions:

---

5. Subgradient

Examples

• 
• 
• 
• 

---

6. Optimality conditions

凸函数的局部最优等价于全局最优。

第一充要条件（凸函数） $x^{\ast }\in \mathbf{dom}f$ is the minimizer $⟺$ $0\in \partial f(x^{\ast })$

---

7. Strong convexity

A differentiable function f is strongly convex if

$$f(y)\ge f(x)+\nabla f(x{)}^T(y-x)+\frac{\mu }{2}\Vert y-x{\Vert }^2$$

Note

1. $f$ is not necessarily differentiable, (see the equivalent definition)
2. if $f$ is non-smooth, gradient → subgradient
3. strong convexity $⟹$ strict convexity

Note: Intuitively speaking, strong convexity means that there exists a quartic lower bound on the growth of the function.

Equivalent definition

$$\begin{array}{rl}& (i)f(y)\ge f(x)+\nabla f(x{)}^T(y-x)+\frac{\mu }{2}\Vert y-x{\Vert }^2,\forall x,y.\\ & (ii)g(x)=f(x)-\frac{\mu }{2}\Vert x{\Vert }^2\text{is convex},\forall x.\\ & (iii)⟨\nabla f(x)-\nabla f(y),x-y⟩\ge \mu \Vert x-y{\Vert }^2,\forall x,y.\\ & (iv)f(\alpha x+(1-\alpha )y)\le \alpha f(x)+(1-\alpha )f(y)-\frac{\alpha (1-\alpha )\mu }{2}\Vert x-y{\Vert }^2,\alpha \in [0,1].\\ & (v){\nabla }^{2}f(x)⪰\mu \mathbf{I}\end{array}$$

---

---

Lagrange Duality

Consider an optimization problem in standard form (not necessarily convex)

$$\begin{array}{ll}\underset{x}{\mathrm{minimize}}& f_0(x)\\ \text{subject to}& f_i(x)\le 0,i=1,\cdots ,m\\ & h_i(x)=0,i=1,\cdots ,p\end{array}$$

The Lagrangian is

$$L(x,\mathbf{\lambda },\mathbf{\mu })=f_0(x)+\sum _{i=1}^m{\lambda }_i{f}_i(x)+\sum _{i=1}^p{\mu }_i{h}_i(x)$$

The Lagrange dual function is defined as

$$g(\lambda ,\mu )=\underset{x}{\inf }L(x,\lambda ,\mu )$$

Lagrange dual problem

$$\begin{array}{ll}\underset{\lambda ,\mu }{\mathrm{maximize}}& g(\lambda ,\mu )\\ \text{subject to}& \mathbf{\lambda }⪰0\end{array}$$

Weak duality

$$d^{\ast }\le p^{\ast }$$

• $d^{\ast }$: optima of dual problem
• $p^{\ast }$: optima of primal problem
• duality gap: $p^{\ast }-d^{\ast }$
• always hold

Strong dualiy

$$d^{\ast }=p^{\ast }$$

• constraint qualifications $⟹$ strong duality
• Slater’s Constraint Qualification: a convex problem is strictly feasible (i.e., $\exists x\in \mathbf{int}\mathcal{D}:x\in \Omega$)

Complementary slackness

KKT conditions

---

---

Cones

Tagent cone Let M be a (nonempty) convex set and $x^{\ast }\in M$, the tagent cone of $M$ at $x^{\ast }$ is the cone

$$\begin{array}{rl}{T}_M(x^{\ast })& =\{h\in {\mathbb{R}}^n|x^{\ast }+th\in M,\forall t>0\}\\ & =\{y\in {\mathbb{R}}^n|y-x^{\ast }\in M\}\end{array}$$

Note:

• Geometrically, this is the set of all directions leading from $x^{\ast }$ inside $M$
• convex but not necessarily closed
• fact: if $x^{\ast }$ is a minimizer, then $\forall h\in T_M(x^{\ast })⟹h^T\nabla f(x^{\ast })\ge 0$. （因为tangent cone里面都是可行解，所以必须不是下降方向）
• $T_M(x^{\ast })={\mathbb{R}}^n⟺x^{\ast }\in \mathbf{int}M$

e.g. 多面体

$$M=\{x|Ax\le b\}=\{x|a_i^{T}x\le b_i,i=1,\dots ,m\}$$

the tangent cone at $x^{\ast }$ is

$$T_M(x^{\ast })=\{h|a_i^{T}h\le 0,\forall i,a_i^T{x}^{\ast }=b_i\}$$

---

Normal cone: the polar cone of tangent cone

$$N_M(x^{\ast })=\{g\in {\mathbb{R}}^n|⟨g,y-x^{\ast }⟩\le 0,\forall y\in M\}$$

Note:

• normal cone is the polar to tangent cone, i.e.,

$$\begin{array}{rl}{T}_M(x^{\ast })& =\{g\in {\mathbb{R}}^n|⟨g,y-x^{\ast }⟩\ge 0,\forall y\in M\}\\ N_M(x^{\ast })& =\{g\in {\mathbb{R}}^n|⟨g,y-x^{\ast }⟩\le 0,\forall y\in M\}\end{array}$$

• fact: if $x^{\ast }$ is a minimizer, then $-\nabla f(x^{\ast })\in N_M(x^{\ast })$.
• 

---

---

Algorithm convergence

~	Stepsize Rule	Convergence Rate	Iteration Complexity
Gradient descent
strongly convex & smooth	${\eta }_t=\frac{2}{\mu +L}$	$O{\left(\frac{\kappa -1}{\kappa +1}\right)}^t$	$O\left(\frac{\log \frac{1}{ϵ}}{\log \frac{\kappa +1}{\kappa -1}}\right)$
convex & smooth	${\eta }_t=\frac{1}{L}$	$O(\frac{1}{\sqrt{t}})$	$O(\frac{1}{ϵ})$
Frank-Wolfe
(strongly) convex & smooth	${\eta }_t=\frac{1}{t}$	$O(\frac{1}{\sqrt{t}})$	$O(\frac{1}{ϵ})$
Projected GD
convex & smooth	${\eta }_t=\frac{1}{L}$	$O(\frac{1}{\sqrt{t}})$	$O(\frac{1}{ϵ})$
strongly convex & smooth	${\eta }_t=\frac{1}{L}$	$O\left((1-\frac{1}{\kappa }{)}^t\right)$	$O(\kappa \log \frac{1}{ϵ})$
Subgradient method
convex & Lipschitz	${\eta }_t=\frac{1}{\sqrt{t}}$	$O(\frac{1}{\sqrt{t}})$	$O(\frac{1}{{ϵ}^2})$
strongly convex & Lipschitz	${\eta }_t=\frac{1}{t}$	$O\left(\frac{1}{t}\right)$	$O(\frac{1}{ϵ})$
Proximal GD
convex & smooth (w.r.t. $f$)	${\eta }_t=\frac{1}{L}$	$O(\frac{1}{t})$	$O(\frac{1}{ϵ})$
strongly convex & smooth (w.r.t. $f$)	${\eta }_t=\frac{1}{L}$	$O\left((1-\frac{1}{\kappa }{)}^t\right)$	$O(\kappa \log \frac{1}{ϵ})$